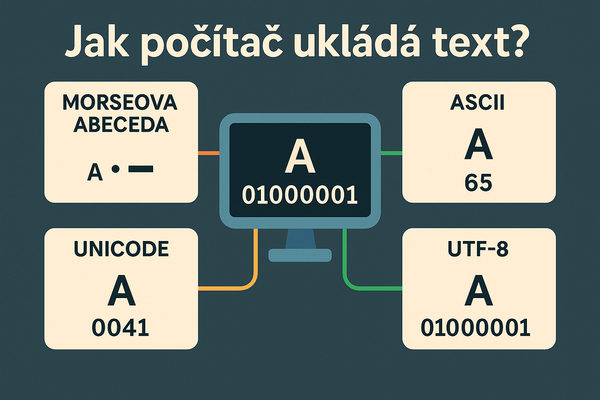
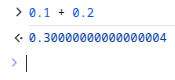
Jak počítač reprezentuje čísla? 0.1 + 0.2 = 0.30000000000000004
Proč počítač spočítá 0.1 + 0.2 jako 0.30000000000000004? Tento článek krok za krokem ukazuje, jak počítač reprezentuje čísla, proč vznikají zaokrouhlovací chyby a jak funguje standard IEEE 754 pro čísla s plovoucí desetinnou čárkou.

Již nějakou dobu učím programování a tento problém zaujme většinu studentů. Většinou to podávám jako dogma, protože bych na vysvětlení zabil příliš mnoho času a bez precizní přípravy bych se do toho mohl zamotat. A koneckonců pro běžného programátora to je zanedbatelný problém.
Nejste programátoři a chcete si to vyzkoušet? Nu dobrá, napíšu vám rychlý návod. Pokud jste na počítači stiskněte na klávesnici F12.
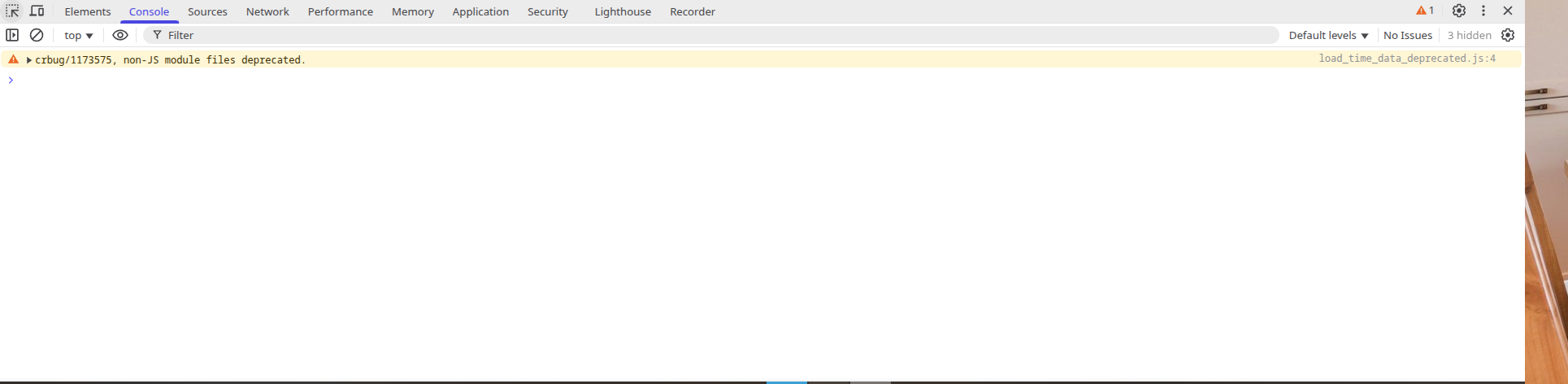
Dostanete okno, které vidíte na obrázku. Na horním panelu se přepněte do Console (na obrázku svítí modře). Největší část obrázku zabírá editor. Kam zadejte 0.1 + 0.2 stisknete Enter a voilà chyba je na světě.
Právě jsem vás naučil základy programování v JavaScriptu.
Jak tedy počítač reprezentuje čísla?
Asi není žádným překvapením, že počítač ve své podstatě „rozumí“ pouze jedničkám a nulám, tedy elektrickým signálům. Když elektřina proudí, můžeme to chápat jako jedničku, a když neproudí, označíme to nulou. Ve skutečnosti sice napětí nikdy není přesně nulové, ale pro naše vysvětlení to nyní není podstatné.
Možná jste už slyšeli, že dnešní počítače používají 64bitové operační systémy. Bit je základní jednotka informace a může nabývat hodnoty 0 nebo 1. Procesor tak dokáže pracovat s „úsekem“ dlouhým 64 bitů. Každý bit má dvě možné hodnoty, takže pro 2 bity existují 2 × 2 = 4 kombinace a pro 64 bitů dokonce 264=1,8×1019 různých kombinací.
Máme dva typy čísel
Určitě si to pamatujete z matematiky. Nejprve se seznamujeme s přirozenými čísly (1, 2, 3, 4, 5, ...), a pak s překvapením zjistíme, že existují i záporná čísla, kterým říkáme celá čísla. Později přijdou na řadu racionální, iracionální, reálná a nakonec i komplexní čísla. Já se ale zastavím především u celých čísel (anglicky integer) a reálných čísel, která počítač reprezentuje jako čísla s plovoucí desetinnou čárkou.
Celá čísla
Celá čísla jsou reprezentovaná u každého jazyka trochu jinak. Pojďme se podívat na jazyk C, který se dá považovat jako standard nízkoúrovňových jazyků. V tomto jazyce si můžeme vybrat kolik bitů pro dané číslo potřebujeme a jestli chci pouze přirozená čísla (nezáporná) nebo celá čísla (záporná i kladná). Nejjednodušší je případ, kdy chci osmibitové nezáporné číslo. Nezápornému číslu se říká unsigned. V takovém případě mohu reprezentovat čísla 0 až 255, protože pro každý bit mám dvě možnosti a mám celkem 8 políček, kde se mohu rozhodnout (2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 = 28 = 256).
Celá čísla jsou v různých programovacích jazycích reprezentována trochu odlišně. Podívejme se na jazyk C, který lze považovat za standard mezi nízkoúrovňovými jazyky.
V C si můžeme zvolit, kolik bitů bude číslo zabírat, a také zda chceme pracovat pouze s nezápornými (přirozenými) čísly, nebo i se zápornými.
Nejjednodušším případem je osmibitové nezáporné číslo. Takovému číslu se říká unsigned. V tomto případě můžeme reprezentovat hodnoty od 0 do 255, protože každý bit může nabývat dvou hodnot (0 nebo 1) a máme jich osm:
2×2×2×2×2×2×2×2=28=256
Celkem tedy existuje 256 různých kombinací, z nichž nejnižší je 0 a nejvyšší 255.
Podíváme se jak jednotlivá čísla zapíšeme.
| Desítkově | Binárně |
|---|---|
| 0 | 00000000 |
| 1 | 00000001 |
| 2 | 00000010 |
| 42 | 00101010 |
| 128 | 10000000 |
| 200 | 11001000 |
| 255 | 11111111 |
Převod do binární soustavy a zpět
Číslo z desítkové soustavy převedeme do binární podoby následovně. Budeme dělit číslo dvojkou a zapíšeme si výsledek ve formátu celé číslo a zbytek. Číslo, které zbylo znovu vydělíme dvěma a postup zopakujeme až do doby, kdy již nelze dále dělit.
Zde si ukážeme jak převést číslo 42:
| Dělení | Celé číslo | Zbytek |
|---|---|---|
| 42 ÷ 2 | 21 | 0 |
| 21 ÷ 2 | 10 | 1 |
| 10 ÷ 2 | 5 | 0 |
| 5 ÷ 2 | 2 | 1 |
| 2 ÷ 2 | 1 | 0 |
| 1 ÷ 2 | 0 | 1 |
Když se podíváme do tabulky převodu na binární soustavu, nejdůležitější je sloupec „Zbytek“ – právě ten představuje výsledné binární číslo. Zbytky zapisujeme odspodu nahoru, takže získáme:
101010
Vidíme ale, že máme pouze 6 pozic, zatímco naše číslo má být 8bitové. Proto doplníme dvě nuly na začátek, abychom dostali plnou osmibitovou reprezentaci:
00101010
Reverzní postup (binární → desítkové)
Každá pozice v binárním zápisu odpovídá mocnině dvojky, počítáno zprava doleva (od nejnižšího bitu k nejvyššímu):
| Pozice | Mocnina | Hodnota |
|---|---|---|
| 0 | 2⁰ | 1 |
| 1 | 2¹ | 2 |
| 2 | 2² | 4 |
| 3 | 2³ | 8 |
| 4 | 2⁴ | 16 |
| 5 | 2⁵ | 32 |
| 6 | 2⁶ | 64 |
| 7 | 2⁷ | 128 |
U našeho osmibitového zápisu 0 0 1 0 1 0 1 0 (zleva bity pro 2⁷ až 2⁰) vynásobíme každý bit příslušnou mocninou dvojky a sečteme:
0 × 2⁷ + 0 × 2⁶ + 1 × 2⁵ + 0 × 2⁴ + 1 × 2³ + 0 × 2² + 1 × 2¹ + 0 × 2⁰
= 0 × 128 + 0 × 64 + 1 × 32 + 0 × 16 + 1 × 8 + 0 × 4 + 1 × 2 + 0 × 1
= 32 + 8 + 2
= 42
Záporná čísla a přetečení
Procesor ve skutečnosti vůbec nezná pojem „mínus jedna“. Stále pracuje pouze s nulami a jedničkami. Jak tedy v binární soustavě reprezentovat záporná čísla?
V desítkové soustavě víme, že platí například:
(+5) + (–5) = 0.
Podívejme se, jak by podobný princip mohl fungovat v binární soustavě.
Číslo 5 v osmibitové reprezentaci zapíšeme takto:00000101
Teď chceme najít takové číslo, které bychom k němu přičetli, aby výsledek byl nula.
Kdybychom použili čistě opačné bity, tedy „jedničky místo nul a nuly místo jedniček“, dostaneme tzv. jedničkový doplněk:
00000101
+ 11111010------------
11111111
Výsledkem je číslo, jehož všechny bity jsou jedničky — to znamená maximální hodnotu, kterou lze s 8 bity vyjádřit (v desítkové soustavě je to 255).
A teď přijde klíčový moment:
co se stane, když k tomuto číslu přičteme ještě 1?
11111111 + 1 = 00000000
Došlo k tzv. přetečení — nejvyšší bit „přetekl“ mimo rozsah a výsledek se znovu vynuloval.
V jazyce C se tento jev označuje jako overflow.
A právě tento princip můžeme využít pro záporná čísla.
V běžné praxi se používá tzv. dvojkový doplněk (angl. two’s complement).
Ten se získá tak, že:
- vezmeme kladné číslo,
- všechny bity otočíme (0 → 1, 1 → 0),
- a nakonec přičteme 1.
Tak například číslo –5 se zapíše takto:
00000101 → původní číslo 5
11111010 → jedničkový doplněk
+ 1------------
11111011 → dvojkový doplněk (reprezentace –5)
Pokud nyní k tomuto číslu přičteme 00000101, výsledek skutečně bude 00000000.
Tímto způsobem počítač umí pracovat se zápornými čísly – aniž by „rozuměl“ znaménku mínus.
Jak počítač čte záporná čísla?
První bit reprezentuje znaménko. 0 je kladné číslo, 1 je záporné číslo. To vyplývá z principu doplňku. 8bitové signed číslo tedy může nabývat hodnot -128 do 127. Co tedy počítač udělá, aby správně reprezentovalo číslo. Podívá se na první bit. Pokud je 0, tak čte číslo jak jsme si již ukázali. Pokud je první bit 1, tak počítač ví, že se jedná o záporné číslo a musí udělat následující kroky:
- Odečíst jedničku
11111011
-00000001
---------
11111010- Udělat inverzi
11111010
-> inverze
--------
00000101- Převést na desítkovou soustavu
1 * 23 + 1 * 20 = 5
- Připsat znaménko -.
Výsledek je -5.
Celá čísla v jazyce Python
Na rozdíl od jazyka C, kde si programátor volí přesnou velikost čísla (například 8, 16 nebo 32 bitů) a rozhoduje, zda bude číslo se znaménkem nebo bez něj, jazyk Python pracuje s typem int jinak.
Python používá pro všechna celá čísla jeden univerzální datový typ, který se chová jako celé číslo s neomezenou přesností. To znamená, že číslo v Pythonu nemá pevný počet bitů. Pokud se hodnota nevejde do běžného 32bitového nebo 64bitového rozsahu, Python si automaticky přidá další bity a číslo zvětší. Díky tomu se v Pythonu nemůže stát přetečení, které by způsobilo, že například 255 + 1 by se stalo 0 jako v jazyce C.
Interně je celé číslo v Pythonu objekt, nikoli pouhý blok bitů. Každé číslo si kromě vlastní hodnoty nese i informaci o svém znaménku a o tom, kolik „číslic“ v binární podobě zabírá. Tyto „číslice“ nejsou jednotlivé bity, ale skupiny bitů – obvykle po 30 bitech na 64bitových systémech. Každé celé číslo je tedy tvořeno znaménkem (kladné nebo záporné), délkou čísla a polem těchto binárních bloků, které dohromady představují jeho hodnotu.
Záporná čísla jsou interně reprezentována v dvojkovém doplňku (two’s complement), stejně jako v jazyce C, ale tento detail uživatel nevidí. Python sám uchovává informaci o znaménku a při práci s čísly se podle ní automaticky řídí. Pro uživatele není důležité, kolik bitů číslo zabírá nebo jak je znaménko uloženo – Python vždy vrací správnou matematickou hodnotu.
Z praktického hlediska to znamená, že:
- všechna celá čísla v Pythonu jsou se znaménkem,
- mohou být libovolně velká, omezená pouze dostupnou pamětí,
- nejsou vystavena přetečení ani ztrátě znaménka,
- a jejich vnitřní reprezentace je spravována interpretem, nikoli programátorem.
Zatímco jazyk C musí rozlišovat, zda má číslo 8, 16 nebo 64 bitů a jak s ním nakládat, Python pracuje s celými čísly na vyšší úrovni abstrakce.
Pro počítač samozřejmě číslo nakonec stále existuje jako posloupnost nul a jedniček, ale Python tyto technické detaily skrývá a místo toho garantuje, že se čísla chovají tak, jak to odpovídá běžné matematice.
Výhody
- Žádné přetečení: Python zvládne libovolně velká čísla, dokud máš dost paměti.
- Jednoduchost: Existuje jen jeden typ
int, nemusíš řešit 8bitové nebo 32bitové varianty. - Bezpečnost: Čísla se nikdy „nepřetečou“ do záporných nebo kladných hodnot omylem.
- Přesnost: Python vždy vrací matematicky správný výsledek.
- Přenositelnost: Kód se chová stejně na všech operačních systémech a architekturách.
Nevýhody
- Pomalejší výpočty: Každé číslo je objekt, ne pouhá hodnota – výpočty tedy trvají déle.
- Vyšší paměťová náročnost: I malé číslo zabírá více bajtů než v nízkoúrovňových jazycích.
- Žádná kontrola nad velikostí: Nemůžeš si zvolit, že chceš 8bitové nebo 16bitové číslo.
- Méně vhodné pro práci s bity: Python nepracuje přímo s pevnou bitovou reprezentací.
- Nevhodný pro nízkoúrovňové programování: Při komunikaci s hardwarem nebo binárními daty je potřeba sahnout po jiných nástrojích nebo jazycích.
Principy zde uvedené platí i pro čísla, která mají více bitů.
Desetinná čísla
Konečně se dostáváme k hlavnímu tématu článku – k tomu, jak jsou v počítači reprezentována desetinná čísla a proč vzniká chyba při výpočtu výrazu 0.1 + 0.2 = 0.3… 4. V tomto případě je situace poměrně přehledná, protože většina programovacích jazyků používá standard IEEE 754. Nemám rád, když se v textu objevují neobjasněné zkratky, proto stojí za to uvést, že IEEE je zkratka pro Institute of Electrical and Electronics Engineers – mezinárodní neziskovou organizaci, která mimo jiné vytváří a spravuje technické standardy.
V této reprezentaci je každé desetinné číslo uloženo v 64 bitech. Než si ale ukážeme, jak jednotlivé bity fungují, pojďme si nejprve vysvětlit, jak vůbec můžeme zapsat libovolné desetinné číslo. Uděláme to rovnou na příkladu. Vezměme si dvě čísla: 1024,5789 a 0,00000000548. Taková čísla lze přepsat do tzv. vědeckého zápisu. Ten funguje tak, že posuneme desetinnou čárku tak, aby před ní zůstala pouze jedna číslice, a ostatní se přesunuly za čárku.
Podívejme se na to konkrétně:
- Číslo 1024,5789 přepíšeme jako 1,0245789 – vidíme ale, že tato dvě čísla nejsou stejná, něco jim chybí.
- Podobně číslo 0,00000000548 přepíšeme jako 5,48 – i zde potřebujeme ještě určit, o kolik jsme čárku posunuli.
K tomu slouží exponent, který udává řád čísla (desítky, stovky, tisíciny atd.). V našem případě:
- 1024,5789 = 1,0245789 × 10³
- 0,00000000548 = 5,48 × 10-9
Pokud si to zadáte do kalkulačky, uvidíte, že výsledky odpovídají. Exponent a mocnina deseti pouze posouvají desetinnou čárku. Právě z tohoto důvodu se těmto číslům v programování říká čísla s plovoucí desetinnou čárkou (floating point numbers).
Převod do binární podoby
Zatím jsme udělali jen malý matematický trik, který se učí na základní škole, ale vždyť počítač rozumí jen 0 a 1. Podíváme se tedy jak převést taková čísla do binární podoby. IEEE754 pro reprezentaci svých čísel používá právě vědecký zápis. A když se podíváme pozorně, tak takový zápis nám přináší tři informace:
- znaménko (+/-)
- desetinné číslo (1,0245789)
- exponent u desítky (3), nebo-li řád čísla
Proto musíme rozdělit 64 bitů na 3 skupiny:
- Znaménko (sign): 1 bit
- Exponent: 11 bitů (udává řád čísla)
- Mantisa: 52 bitů (udává vlastní číslo)
Pro exponent tedy máme 211 = 2048 možností, protože máme kladné a záporné možnosti, tak je to interval od -1021 do 1024. (-1023 a -1022 je rezerovaný). Pro mantisu (samotné číslo) máme 252 = 4,5 * 1015 možností.
Jak je tedy číslo v binární podobě reprezentováno?
Desetinné číslo je reprezentováno v následující podobě:
(−1)sign× 1.mantisa × 2exponent-1023
Ukažme si příklad jak převedeme desetinné číslo na binární podobu. Začneme s číslem, které má jednoduchou binární podobu a to je číslo 6.25.
Zde je algoritmus:
- Rozdělíme číslo na celou a desetinnou část
6.25=6+0.25
- Celou část převedeme klasicky dělením dvojkou
| Dělení | Zbytek |
|---|---|
| 6 ÷ 2 = 3 | 0 |
| 3 ÷ 2 = 1 | 1 |
| 1 ÷ 2 = 0 | 1 |
V binární soustavě se 6 zapíše jako: 110
- Desetinnou část převedeme násobením dvojkou
| Krok | Číslo × 2 | Celá část | Nová desetinná část |
|---|---|---|---|
| 1 | 0.25 × 2 = 0.5 | 0 | 0.5 |
| 2 | 0.5 × 2 = 1.0 | 1 | 0.0 |
V binární soustavě se 0.25 zapíše jako: 0.01
- Spojíme obě části
110 + 0.01 = 110.01
- Posuneme desetinnou tečku
Musíme posunout desetinnou tečku, tak aby byla před tečkou jen jedna číslice a to je jednička. Tím dostaneme číslo 1.1001 × 2něco . Podobně jako u desítkové soustavy používáme "vědecký" zápis, s tím rozdílem, že násobíme dvojkou, kterou umocníme na něco. Protože jsme již v binární soustavě, tak to něco bude počet řádů o kolik jsme tečku posunuli, takže je to 1.1001 × 22 .
- Zjistíme mantisu
Z tohoto zápisu již můžeme vyčíst mantisu, to je to číslo, které je za tečkou a doplnit ho do 52 míst nulami, takže mantisa je:
1001000000000000000000000000000000000000000000000000- Spočítáme exponent
Můžeme si všimnout, že v tomto zápise 1.1001 × 22 mám stále exponent v desítkové soustavě. Musíme ho převést na binární. Řekli jsme si, že exponent může nabývat 2048 hodnot. Chceme mít i záporné exponenty a nulu uprostřed, takže může nabývat 1023 kladných hodnot. Počítač neumí pracovat se zápornými exponenty, proto musíme k exponentu připočíst + 1023, tak aby vždy nabýval kladných hodnot. V našem příkladu máme exponent rovný 2. Počítač pak exponent reprezentuje jako 2 + 1023 = 1025. V binární podobě je 1025 znázorněný takto:
10000000001- Vyznačíme znaménko +/-
První bit celé reprezentace určuje znaménko. Pro kladné číslo je 0, pro záporné číslo -1.
- Vytvoříme celý binární zápis
0 10000000001 1001000000000000000000000000000000000000000000000000
znménko | exponent | mantisaProč tedy součet 0.1 + 0.2 není přesně 0.3?
Převod čísla 0.1
- Rozdělíme číslo
0.1 = 0 + 0.1
Celá část je 0 → v binární soustavě:0. - Desetinnou část převedeme násobením dvojkou
| Krok | Číslo × 2 | Celá část | Nová desetinná část |
|---|---|---|---|
| 1 | 0.1 × 2 = 0.2 | 0 | 0.2 |
| 2 | 0.2 × 2 = 0.4 | 0 | 0.4 |
| 3 | 0.4 × 2 = 0.8 | 0 | 0.8 |
| 4 | 0.8 × 2 = 1.6 | 1 | 0.6 |
| 5 | 0.6 × 2 = 1.2 | 1 | 0.2 |
Vidíme, že se desetinná část opakovaně vrací k 0.2 → vzniká nekonečný periodický rozvoj:
3. Normalizace
Posuneme čárku tak, aby vlevo byla jedna jednička:
1.10011001100… × 2-4
- Mantisa
Vezmeme čísla za tečkou a usekneme je na 52. bitu (přesně tady vzniká chyba):
1001100110011001100110011001100110011001100110011001
- Exponent
Reálný exponent = −4
Bias = 1023
→ uložený exponent = −4 + 1023 = 1019
→ binárně: 01111111011
- Znaménko
Kladné číslo → sign = 0
- Výsledná reprezentace
| Část | Bity |
|---|---|
| sign | 0 |
| exponent | 01111111011 |
| mantisa | 1001100110011001100110011001100110011001100110011001 |
0 01111111011 1001100110011001100110011001100110011001100110011001
64bitový zápis:
0011111110111001100110011001100110011001100110011001100110011010
Převod čísla 0.2
- Rozklad
0.2 = 0 + 0.2 - Převod desetinné části
| Krok | Číslo × 2 | Celá část | Nová desetinná část |
|---|---|---|---|
| 1 | 0.2 × 2 = 0.4 | 0 | 0.4 |
| 2 | 0.4 × 2 = 0.8 | 0 | 0.8 |
| 3 | 0.8 × 2 = 1.6 | 1 | 0.6 |
| 4 | 0.6 × 2 = 1.2 | 1 | 0.2 |
Opět vzniká perioda:
0.2 = 0.00110011001100…
- Normalizace
1.10011001100… × 2-3
- Mantisa
1001100110011001100110011001100110011001100110011001
- Exponent
Reálný exponent = −3
Bias = 1023
→ uložený exponent = 1020
→ binárně: 01111111100
- Znaménko
Kladné číslo → sign = 0
- Výsledná reprezentace
| Část | Bity |
|---|---|
| sign | 0 |
| exponent | 01111111100 |
| mantisa | 1001100110011001100110011001100110011001100110011001 |
64bitový zápis:
0011111111001001100110011001100110011001100110011001100110011010
Čísla na závěr sečteme
Cíl: Sečíst 0.1 + 0.2 tak, jak to provádí počítač podle standardu IEEE 754 double (binary64), a převést výsledek krok po kroku na desítkovou hodnotu.
1. 64bitová reprezentace obou čísel
| Číslo | Hex | Binární zápis (sign + exponent + mantisa) |
|---|---|---|
| 0.1 | 0x3FB999999999999A |
0 01111111011 1001100110011001100110011001100110011001100110011010 |
| 0.2 | 0x3FC999999999999A |
0 01111111100 1001100110011001100110011001100110011001100110011010 |
2. Rozložení na složky
| Číslo | sign | exponent (uložený) | exponent (reálný) | mantisa (s implicitní 1.) |
|---|---|---|---|---|
| 0.1 | 0 | 1019 | −4 | 1.1001100110011001100110011001100110011001100110011010₂ |
| 0.2 | 0 | 1020 | −3 | 1.1001100110011001100110011001100110011001100110011010₂ |
3. Zarovnání exponentů
Menší exponent (−4) musí být zarovnán na větší (−3).
To znamená posunout mantisu čísla 0.1 o jeden bit doprava:
| Číslo | Mantisa po zarovnání | Exponent |
|---|---|---|
| 0.1 | 0.1100110011001100110011001100110011001100110011001101 | −3 |
| 0.2 | 1.1001100110011001100110011001100110011001100110011010 | −3 |
4. Sečtení mantis
1.1001100110011001100110011001100110011001100110011010
+ 0.1100110011001100110011001100110011001100110011001101
--------------------------------------------------------
10.0110011001100110011001100110011001100110011001100111
5. Normalizace výsledku
Výsledek začíná 10., musíme posunout binární čárku o 1 vlevo → zvýšíme exponent o 1.
| Položka | Hodnota |
|---|---|
| Normalizovaná mantisa | 1.00110011001100110011001100110011001100110011001100111 |
| Nový reálný exponent | −3 + 1 = −2 |
| Uložený exponent | −2 + 1023 = 1021 |
| Binárně exponent | 01111111101 |
6. Sestavení výsledku
| Část | Bity |
|---|---|
| sign | 0 |
| exponent | 01111111101 |
| mantisa | 00110011001100110011001100110011001100110011001100111 |
Plný 64bitový výsledek:
0 01111111101 00110011001100110011001100110011001100110011001100111
8. Převod zpět na desetinné číslo
IEEE 754 tvar:
(−1)0 × 1.001100110011… × 2-2
Výpočet:
1.001100110011₂ = 1.199999999999999310
1.1999999999999993 × 2−2 = 0.2999999999999998
Skutečně uložený výsledek v paměti je 0.2999999999999998. Jak se z něho stane 0.30000000000000004 si ukážeme příště.
P. S.: Nakonec je z toho velmi dlouhý článek. Jsem rád, že při přednáškách tento aspekt nevysvětluji, protože je to pokročilé téma, které by zabralo spoustu času a je zde velký prostor se zamotat.